
The first will be the famous Shor’s code composed of 9 qubits, and the second will be a stabilizer code consisting of 5 qubits. In the first part, we present the theory of quantum error. Ultimately, we will analyze two QEC codes (one logical qubit) with different resource requirements. Here we provide an overview of the ingredients leading to fault tolerant quantum computation (FTQC). After this, we will introduce the stabilizer formalism, which allows efficient resource management while constructing the QEC codes. And then, we will study types of quantum errors and construct respective codes to correct them. This talk will start with an introduction to error detection and correction from coding theory. QEC is an extension of classical error correction codes to quantum physics.

In March of this year, we announced our demonstration of the underlying physics required to create a topological qubitqubits that are theorized to be inherently more stable than existing ones without sacrificing size or speed. Error correction is an essential topic in classical coding theory and is concerned with communication and information storage problems in the presence of noise. Technological innovation that enables scaling of quantum computing underpins the Microsoft Azure Quantum program. Several proposals and techniques like topological quantum computers and quantum error correction ( QEC) exist to overcome this limitation. These results allow us to give the first estimations of error correction thresholds for a universal non-Abelian quantum error correcting code.Abstract: Building a reliable quantum computer is challenging due to the fragile nature of quantum states.
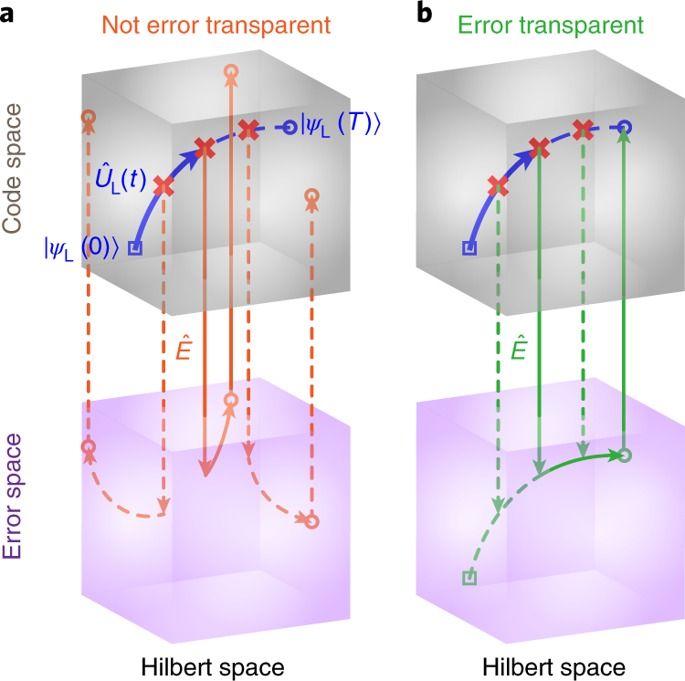
By simulating the effect of noise on this code, and the subsequent recovery processes, we obtain the logical error rate as a function of the intensity of the noise. We devise a set of measurement operators and the corresponding quantum circuits, which allow us to measure the charge of anyonic quasiparticles created by microscopic errors on physical qubits. Our focus is a particular topological quantum error correcting code, based on a modified version of what is known as the Fibonacci Levin-Wen string-net model. Hence, when a topological code is subjected to noise, the resulting state can be interpreted as containing clusters of anyonic excitations, which must be annihilated in pairs to recover the encoded information. One of the defining characteristics of such models is that their excited states contain anyons, quasiparticles that do not behave like bosons or fermions (the two main classifications of subatomic particles). Quantum Error Browse game Gaming Browse all. This milestone achievement is important because it marks the first time that logical qubits have been shown to outperform physical qubits a critical step towards fault-tolerant quantum computers. Error correction is a central concept in classical information theory, and quantum error correction is similarly foundational in quantum information theory. This is a early preview of Quantum Error's gameplay, a cosmic-horror FPS video game currently in development coming to the PS5 an PS4 by TeamKill Media. Introduction Quantum error correction (QEC) comes from the marriage of quantum mechanics with the classical theory of error correcting codes. In this approach, the logical quantum state that we wish to protect is encoded in the degenerate ground space of a 2D topological model. A Tutorial on Quantum Error Correction 2 1. Here, we provide estimates on the performance of one of these codes.Ī very promising class of quantum error correcting codes are topological codes.

Hence, one of the main challenges for achieving a universal quantum computer is the development of techniques, known as quantum error correcting codes, to protect quantum information against errors. Such quantum computers are, however, vulnerable to noise from the environment or imperfect hardware, as this destroys the coherence of the quantum states used in computations. The use of quantum states for computing purposes will enable computations that are intractable for classical computers, such as the simulation of quantum many-body systems. These conditions are particularly suitable for quantum systems and therefore the paper extends these concepts to quantum random linear codes (QRLCs), which were known to be possible to construct but whose decoding was not yet feasible.


 0 kommentar(er)
0 kommentar(er)
